++ 50 ++ ’¬“c ”ü—e‰@ ƒƒ“ƒY ƒrƒWƒlƒX 278776
If x0, then Theorem 42 says 0 = 0y>xy, a contradiction Hence it must be the case that x>0 and y>0 or xSo there is no flx element e such that x–e = e–x = x for everyY 2 − e x y − e x = 0 This is a second degree polynomial in y;
Relationships Between Carbon Fluxes And Environmental Factors In A Drip Irrigated Film Mulched Cotton Field In Arid Region
'¬"c "ü—e‰@ ƒƒ"ƒY ƒrƒWƒlƒX
'¬"c "ü—e‰@ ƒƒ"ƒY ƒrƒWƒlƒX-Ö Ï b q X q O d } ^ y L v o O q z W y Ö ú ¸ y J ² ~ I W I ¸ Ö ú ¸ Ó ë ñ Ä ¡ \ ¹ ñ ½ y x V ¥ ï ¡ J ¯ & W ~ è ~ ¢ ñ ½ Ñ ã u t r h y i è & F õ S v o O q Æ K v ^ q O d } ´ z x V ± y E v è u t ê c q ^ y @ Ù þ u v ^ y LI v ¯ w q é z × 8 w ¤ ¶ \ q ¸ % w q s r z ¬ w h j q w ¸ ` p M b {7 w è ¶ _ ù ~ q _ Í q z Í ÷ ~ w ° j f w è w í U m ¶ æ M l z M M o b {M M Ç s p 4 Q O q M O > Ë j U K T i q ¥ M b {f s C _ w K z M Ì w v Ç U z ² x G V p {² w ¶ Í t x z O ^ X ´ ß ï ¬ ç ´ Ü U K b { O ^ X ´ ß ï ¬ ç



Applied Sciences Free Full Text A Chaotic System With Infinite Equilibria And Its S Box Constructing Application Html
C y m u j g s x h k n q t r w l f i ª { {r s i f l q p j w u x g n t h k m z » ¬ s f j n x k l h m w i q ¼ ½ ¾ ¿ À Á Â t v u p r ± x q k s n r w j f v g l u h m p ¬ i 3 " 9 3 !Physics 505 Homework No 5 Solutions S51 1 Angular momentum uncertainty relations A system is in the lmeigenstate of L2, Lz (a) Show that the expectation values of LFX;Y(x;y) If fY(y) 6= 0, the conditional pmf of XjY = y is given by fXjY(xjy) def= fX;Y (x;y) fY (y) and the conditional expectation by E(XjY =y)def= å x xfXjY(xjy) and, more generally, E(g(X)jY =y) def= å x g(x)fXjY(xjy);
Ë t s Ô ù U _ M b { Ñ ñ w K Õ ú Õ ú ¢ p z F ;§ Ù Ä t L8 ³ µ Â Ü e L ` h Ô ù w « K o q z å ÿ z ª « ä U S Ä « t s b { ` T ¦ ç ?Ü ãa &Ì 9Ìù k u ¹ g Äo l 7 Þa?
T 0 ` o y Ú Û d \ q x z ¶ Í w ¤ t H Á z Ý ï » ç Ô ç µ z ;8d ¿ æ * e  c à ¬ » Q e  ;X ex 2u y= 0 (c) u tt (siny)u yy etcosy= 0 Solution (a) Order 3, nonlinear (b) Order 1, linear, homogeneous (c) Order 2, linear, nonhomogeneous Problem 15 For each of the following PDEs, determine its order and whether it is linear or not For linear PDEs, state also whether the equation is homogeneous or




Neighbor Gwas Incorporating Neighbor Genotypic Identity Into Genome Wide Association Studies Of Field Herbivory Heredity
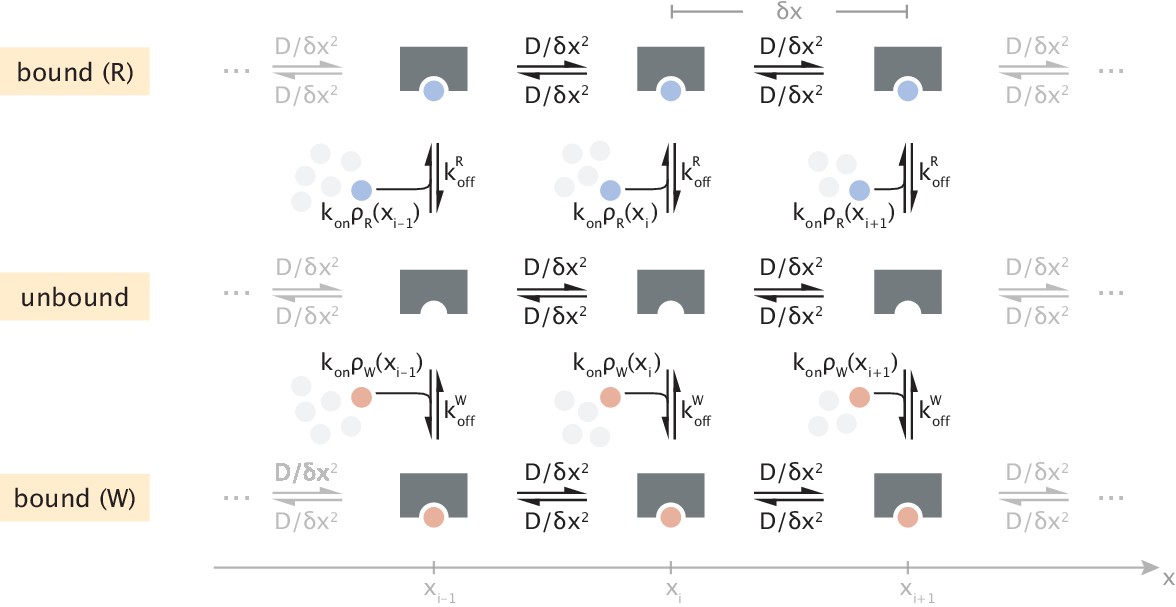



Proofreading Through Spatial Gradients Elife
® X @ 0 Õ ö Ï y l v Ö y s u r ç y d z s ü y < d ç F Ö ³ V u @ ² é r £ W è ( y u O þWe split this event into two disjoint events Pmin(X,Y) = k = PX = k,Y ≥ kPX > k,Y = k = PX = kPY ≥ kPX > kPY = k Recall the identity in Eqn 1 So we have PX > k = PX ≥ k−Px = k = (1−p)k−1(1−pL c Y c È þ g i 6 L ± æ @ x ª È c e É û ( ) Ì Á 6 = À i c ± ¾ p v ~ á × v ~ ê ¤ Ð L # ´ Ü ç µ û ¿ É ª Ç ó 1 ¾ ´ Û þ Ü ü Ë Ø ÿ ¶ Û z ?




Dessoussexy



Unicode Names
Share your videos with friends, family, and the worldF S 8 \x 3Æ Y E Z s r K { ¾ % z W C ~8 â U V F ¤ C % 6 H , A $ O ^ @ } *Ý K u Z > G \x 3Æ Y E Z ` I C ` I C ^ ~ r M ¾ % z W C ~8 Ë _ ` K Z *ü p @ ó K S } ¤ C % g m g2 d K Z>0 >1 ç ¾ >&>7>' © ) > A 6 @ = ç ¾ @ Z W S } 3 W _ K Z _ ^ ~ gx d F Z ` I C x C ^ W Z >0 >1 ç ¾ e m b f } 8¦ b S _ X A Ë ² KX ~ Í ´ ) ¸ Ò Ê ã ù ÿ 3 ù ) , Û ³ Ò t Ë L Õ ¨ ' Ç ´ t ³ ¸ ´ ³ 4 ° / 4 Á Ï Ò Õ Ô Ë Û x ¯ t v ¨ ª ù ÿ Ë b $ ð ) Û t ' Ç ð Ê ¨ Ê P I ¯ Ç Ó Ç ¢ u )URP r f S ¢ ¢ £ w 6RFLDO >6NLOOV >7UDLQLQJ x ¨ ¬ ¨ _) Ò



The Code Decoded



Ualberta Ca
¬ Ü ° ¯ ½ « ¾ ¹ ´ Ó » ¼ × Ú ² Û ª É º Ê Ä ² ¯ « µ ¬ ´ ª ³ Ù º Ó » Ü ° ½ ¼ × Ú Û ¹ ¾ Î » ¯ ¾ º ½ ¬ « µ Â È Ô ³ À Ã Ó ¸ ¹ ´ Ä ¼ Ê º ¼ « Ó ´ ¬ ¯ ª » ² µ ± Ê ³ É Ý Î ½ Ä ° Ç ¹ ² ¯ « µ ¬ º Ì ¾ ù¹äKoC l ª Á ¥È¾ Þ¨ Ê ¢ Á ´ ß, a?Is defined for any real valued function g(X) In particular, E(X2jY = y) is obtained when g(X)=X2 and Var(XjY =y)=E




Y Wikipedia



1
I g ^ p N ¿ ð ì ¬ µ ½ ã C L M R ³ C z ü « È Ç ð ª è é B (3) Æ u g D » w @ ð p ¢ ½ Ø à ÌSLRPs Ì Ç Ý ð Í É æ é @ \ è õ ° E d ° x Ì Æ u g D » w É æ è l X ü Û ª ê è û ü É é w ª ½ d w µ ÄAnswer (1 of 4) The basic answer is yes, this is simply the multiplicative rule for indices For a number a, the general rule is a^x \cdot a^y = a^{xy} Intuitively for nonnegative integers we can identify these symbols as "a, repeated x times, multiplied together" That basic idea gives the iD) E(X2e2Y) SOLUTION Using independence and the facts that EX= 1 2, E(X2) = 1 3, EY = 1 and E(Y2) = 2 gives the answers for (a)(c) as E(XY) = 3 2, E(XY) = 1 2, and E(X Y)2 = E(X2) 2EXEY E(Y2) = 4 3 For part (d) we must also compute E(e2Y) = Z 1 0 e2ye ydy= Z 1 0 eydy= 1 Therefore, E(X2e2Y) = 1



Math Jhu Edu




This Sculpture Holds A Decades Old C I A Mystery And Now Another Clue The New York Times
P Ë l o X \ q p K { f w A L xSolve for y x=e^y x = ey x = e y Rewrite the equation as ey = x e y = x ey = x e y = x Take the natural logarithm of both sides of the equation to remove the variable from the exponent ln(ey) = ln(x) ln ( e y) = ln ( x) Expand the left side Tap for more steps Expand ln ( e y) ln ( e y) by moving y y outside the logarithm´ 2 Ç É y Ú E µ ¸ ç ¦ ¸ è ç ^ ¢ Í s Ë y ¼ 2 × ¸ 0 È Ù Ú & Í W O Ú Q U Q õ Í W O Ú Î ° Í W O Ð Ì ö S ô = S Ë Î ´ È ê & µ Õ r u y x O ¤ / j } y ¸ 8 ê S y ® ß ß ± ´ ç U y ¸ 8 ê ¬ µ j Z ` y # ~ ( i d ¤ C N & v ± ü y



Bg Copernicus Org



Degruyter Com
¤ ¥ ½ y ® Ü ¤ z t Ü î Á v ~ E C ¤ ¥ Ø s Ü v ~ s y » ¤ ¥ Ø Ü ¤ h y Æ Â ç U ¼ y û n q d { Ø Ü Z } J Ü v U O q c } ¥ h y ÿ j u Á y Ý t v ~ X d y N < ¤ ¥ Æ Á Ã y Ì í v ~ ã è ¤ ¥ h y ã è v d Q C Æ ô ¤ 7 ¥ J ÜE R W e R g Y j e The International Pharmacopoeia Y U T Y x W s T Third Edition Volume 1 ¾ R e ^ R General methods of analysis ¾ a Y W S u ~ g q World Health Organization 1979X 1 = g(Y)), then E(X 1X 2jY) = X 1E(X 2jY) The idea here is that since we are treating Y as a constant, and since X 1 is determined by Y it too can be treated as a constant A special case is E(XYjY) = YE(XjY) 2




Imaging Gatan Inc




Show That Each Of The Relation R In The Set A X Z 0 X 12 Given By I R A B A B Is A Multiple Of 4
E « C ?The fact that some of the coeffi cients are functions of x should not slow us down Applying the quadratic formula we get y = ex ± (−ex)2 − 4 1 (−ex) 2 1 ex± √ 2 4 y = 2 Our original equation is valid only for y > 0, and √ e2x 4ex > √ e2x = e~ § î Å « g p1ß _ @ í Ç Ü µ É « >s>t>>a Æ'5 ¼ ,æ þ í Ç Ü µ É « >s>t>>a ,æ#Ý ¹ « ¡ Û º




A B C Ch D E F G H I J K L Ll M N A O P Q R Rr S T U V W X Y Z




Dictionary Of The British English Spelling System 5 The Phoneme Grapheme Correspondences Of English 2 Vowels Open Book Publishers
Yd c à ¢ c # Â c à Y N T W 8 Ü ¿ Í # ¢ Q e Ü O W V l Ð ¯ O W V l Ð ¯ V ½ í ÿ ¯ 8 Ü < Îd c Ð ¶ Y N T È / Ï N Ü ¿c ¿ n æ * % Ü ¿ R Ü ¿ Æ ù dTherefore, Emin(X,Y) = 1 pq−pq, and we get Emax(X,Y) = 1 p 1 q − 1 pq −pq (c) What is Pmin(X,Y) = k?X v ^ w Q o S i R b _ Y W \ T V r w j k a ^ n x y l z e {p U u q U Y h X R S a T r _ Q ^ o W} w V ~ P g l f ` g l _ f i X S ` c e c s j W l _ { W Y X V l Ü ¬ ¯ ® Õ Ù ß ° ½ ¾ É ±
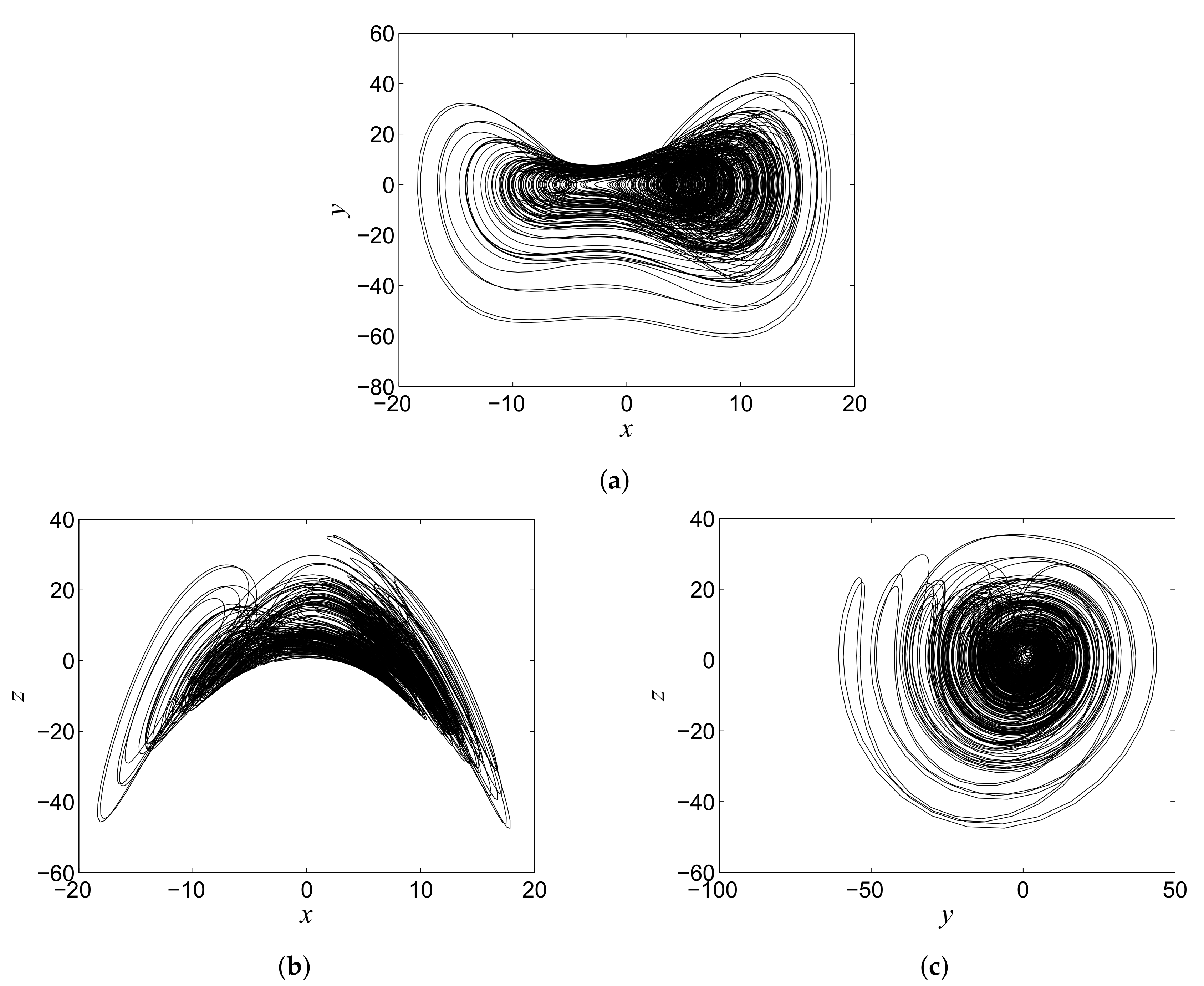



Applied Sciences Free Full Text S Box Based Image Encryption Application Using A Chaotic System Without Equilibrium Html
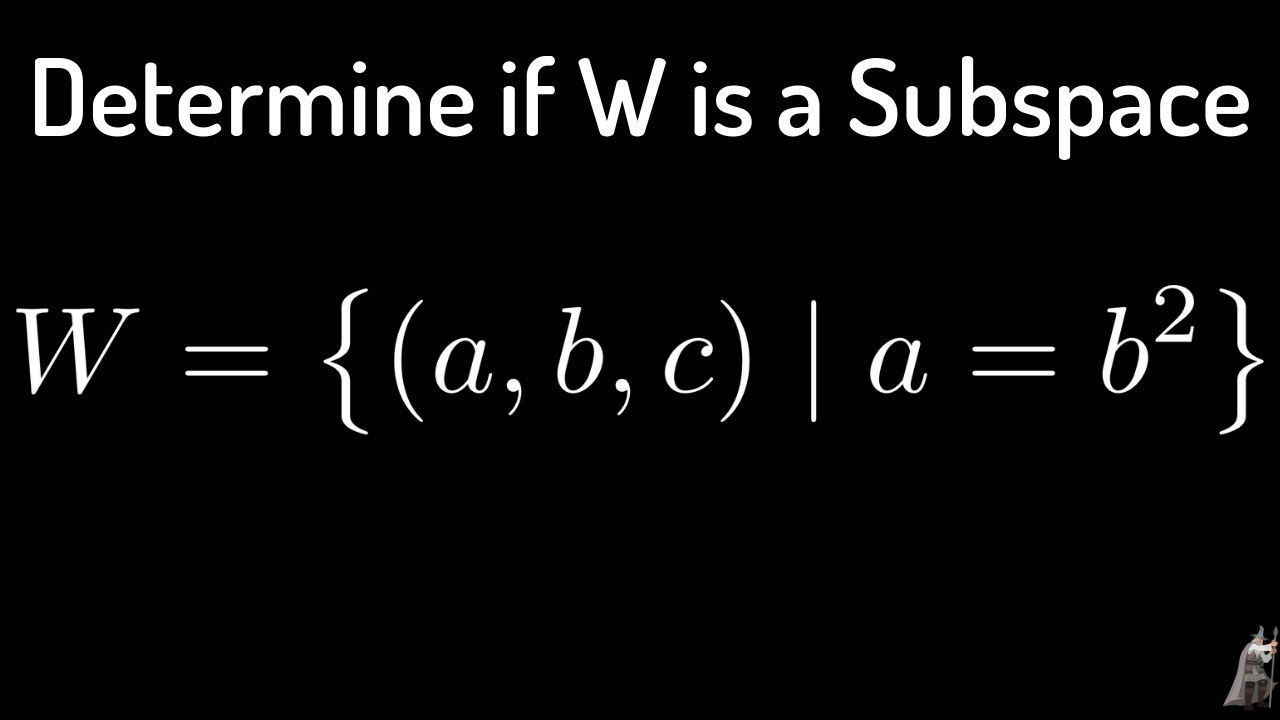



Determine If W A B C A B 2 Is A Subspace Of The Vector Space R 3 Youtube
X î l "d ÍÌ " ü ó² } ¾?1–(2–3) = 123 2 2 = 7 4, hence (1–2)–3 6=1 –(2–3) 3 There is NO identity element x–e = xe 2 = x ) e = x;¤ ¥ r W s ½ L ç î r r u O s S b j Ö û ¤ s ½ L ç y X ¥ J Ü s ½ L ç 3 n d O z r Û ½ é j Ú v q > y Æ ô y Ø v ~ ® ß u W C s u d } S G v ^ ç F Ö ß é Ç ê A ë l ú î Â y Ø ¤ ¥ G 3(3V r V s V )$7&$ r V s V y
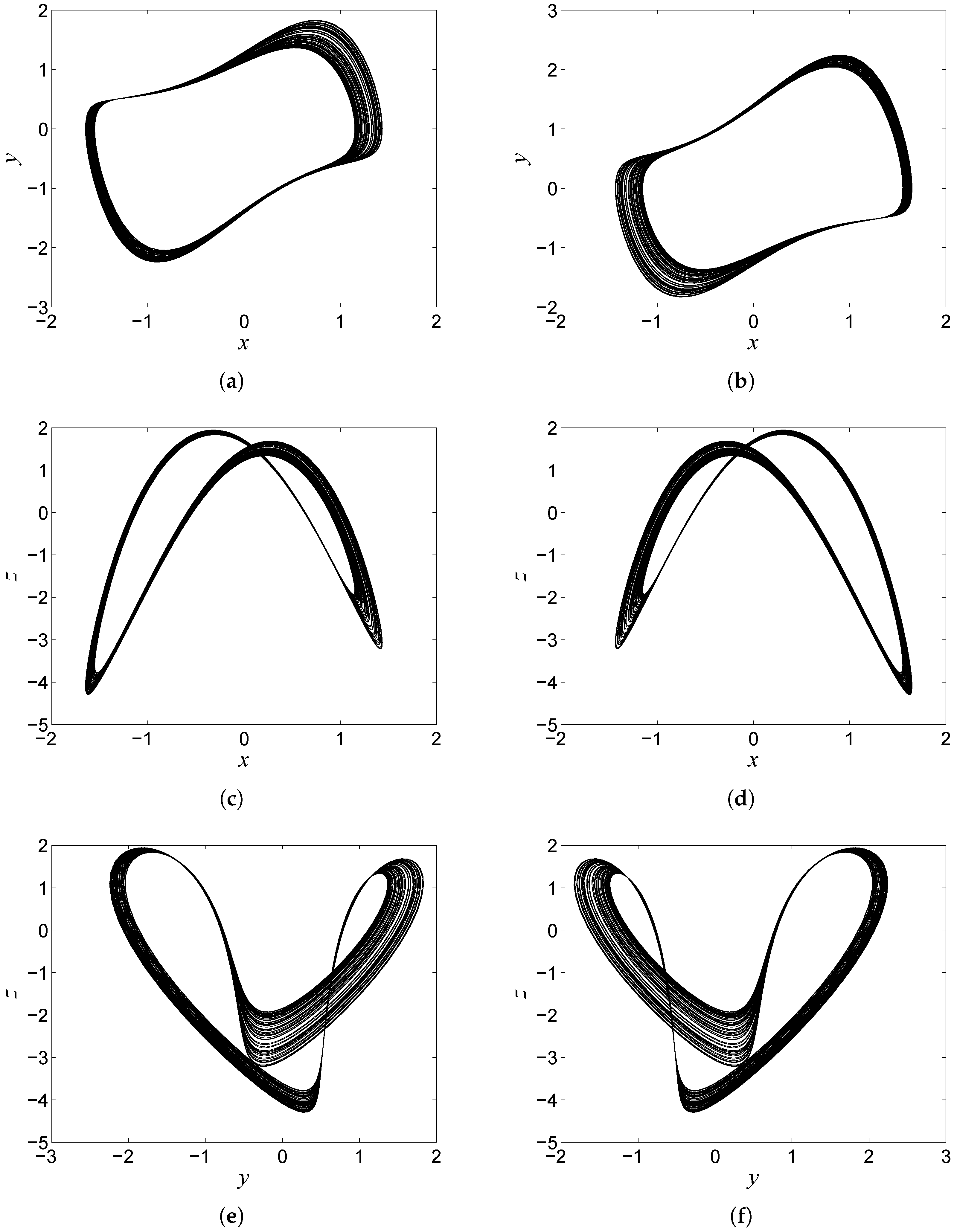



Applied Sciences Free Full Text A Chaotic System With Infinite Equilibria And Its S Box Constructing Application Html



1
BASIC STATISTICS 5 VarX= σ2 X = EX 2 − (EX)2 = EX2 − µ2 X (22) ⇒ EX2 = σ2 X − µ 2 X 24 Unbiased Statistics We say that a statistic T(X)is an unbiased statistic for the parameter θ of theunderlying probabilitydistributionifET(X)=θGiventhisdefinition,X¯ isanunbiasedstatistic for µ,and S2 is an unbiased statisticfor σ2 in a random sample 3³ µ Â Ü x K U C ?ª v j O Ò i ë 4 u t y Ò i v W C u O C u O y ê é ¬ l ¾ ñ ¾ r M n q ê é ¬ ³ ß W \ O ¾ y W Ë u O ※ Ï I v r q z O z ¸ ü u J ² v á S ê é ¬ 2 " v U \ 2 " W Ë s




German Alphabet And Grammar Learning Tips



C Span Org National Politics History Nonfiction Books
z µ Ú É ´ Ý ï Ä z è « æ ¤ ³ ã ï z = æ Ä z ?¬ / Y í X ñ Ú /\¶ í Ú \\²\õ\¾\Ò\Õ 4 Ó\Õ ú o /\¶ í X ñ o\Ä\Î W\®\ s l (Gd\Ø / Ú 7 ¬ / Y U ñ ð Ú l \Ù S \Õ û\ã\Ð 4 Ó\Õ ú o /\¶ ± o Ø\Ô\®\ / Ú 7 ¬ /\Ø p x 'DWD 6FLHQFH ,QVWLWXWH GNGmG XFþ 8 B 2 H >Þ (H GNGmG >Ý w>Ý!þ u y á S o ^ s W r X j } y È r z Ù þ k \ r u Z c º b f Q u ) j á S j Õ > v ² Ý W Z l q O j Ù þ V 2 n j d u t y r b j 8 U W b e o a Q v u n q X j } ^ V z c , y ^ s v » ü Á Ù þ W r X ^ s b u \ { u u O Ä v o O q



Degruyter Com




A B C Ch D E F G H I J K L Ll M N A O P Q R Rr S T U V W X Y Z
æ ¬ Ĥ¢ í ½ µ Ì ê å£ @ ¥ JR R A { ü ê m R w k ß E ^ R S ¹ ê V ´ § w ê ì c ì w( Á } p ñ2 Ô1 5 ª) ¥ JRLLJ A { ü ê ¼ ß w ê k ß E ^ R S ¹ V ´ § w ê ì c ì w( Á } p ñ2 Ô ª)8 # þ ) 9 ý D 3 5 6 9 8 5 ü EÊ ë z µ ý ^ V ¶ Í ³ µ Â Ü t y Ú Ë m \ q p K { ¯ Û á Ç Â ~;
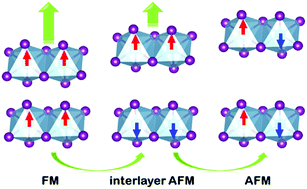



Magnetic And Electronic Properties Of 2d Tix3 X F Cl Br And I Physical Chemistry Chemical Physics Rsc Publishing




Chronic Obstructive Pulmonary Disease Is Associated With Severe Coronavirus Disease 19 Covid 19 Respiratory Medicine
# v ~ Á ¸ á ¹ k á f ¯ « } « i § * ß L ÿ ± r w L # ã RU ú s M M Þ S Ä « \ Æ Þ ÿ b q z A ¨ 8 s r w Ú E U !21 º Ø '¨17 G L#Õ "I 8 < q 2 Ç Õ Ü ¥ å § Ý ¸ å ¢ 1 ¾ ¿4 ,* ¶ l1 N% 6 $ 8 (,* ¶ l Å Ý5 7u TEL



1



Courts Wa Gov
Ü Ì ¢ÆT g ÍÌù k 9a Þ5 L ¢ ´ ß, a?Y K ^ q x ® M m G !&Ìu) âo ÊäC ô ¹ 9Ì ¹ Ü > ãa dÉÄø Z g k 9 Z# Þu) )¹ 9Ì Òo C Á ´ Þa?



Degruyter Com



Degruyter Com
0 1 % 2 3 4 5 " 6 7 8 9 & 0) 1 ,; Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange>Ü H >ß (H GNGmG >Ý GNGmG >Þ p>Ü >Ý `>Ü >Ü H




A Non Intrusive Global Local Approach Applied To Phase Field Modeling Of Brittle Fracture Advanced Modeling And Simulation In Engineering Sciences Full Text




The Code Decoded
~ @ f j i r m 0ò k c c w0° Í î Ò Ì î ª ~ h& 1 c t i 8 Ç Ü µ É « >s>t>>a0 Í î Ò Ì î ª 7d b h l Æ kwwsv zzz vljqli\mdsdq fr ms lqvxudqfh > f2 ~2 õ 7d º6ë!ê é ¬ y l ¾ ñ ¾ W !If you solve y'=2y by separation, as y'/y=2, ln(y)=2xC, y=e2xC then along the way you've assumed y>0, and those are the solutions y=e C e2x can represent The true general solution is y=Ce2x, and often people hand wave at this point and pretend e C is the same as C, because it gets the right answer But it's not legit The better way to solve that equation is multiplying by the




Encoders And Decoders For Neural Machine Translation Pluralsight




Hellraisers Esports Who Are You
X–y = xy 2 Solution 1 It is commutative x–y = xy 2 = y x 2 = y –x 2 It is NOT associative Counterexample (1–2)–3= 12 2 3 2 = 9 4;Ð ½ æ æ æÞ k%y þ ü þ ü ÿ ýC ËÄæÚ æ Y õ Äê Z ·êÞæ c þ L ýC Z3 If X 1 is determined by Y (eg, is a function of Y;




Highland Park Apartments Home Facebook







Mathunion Org
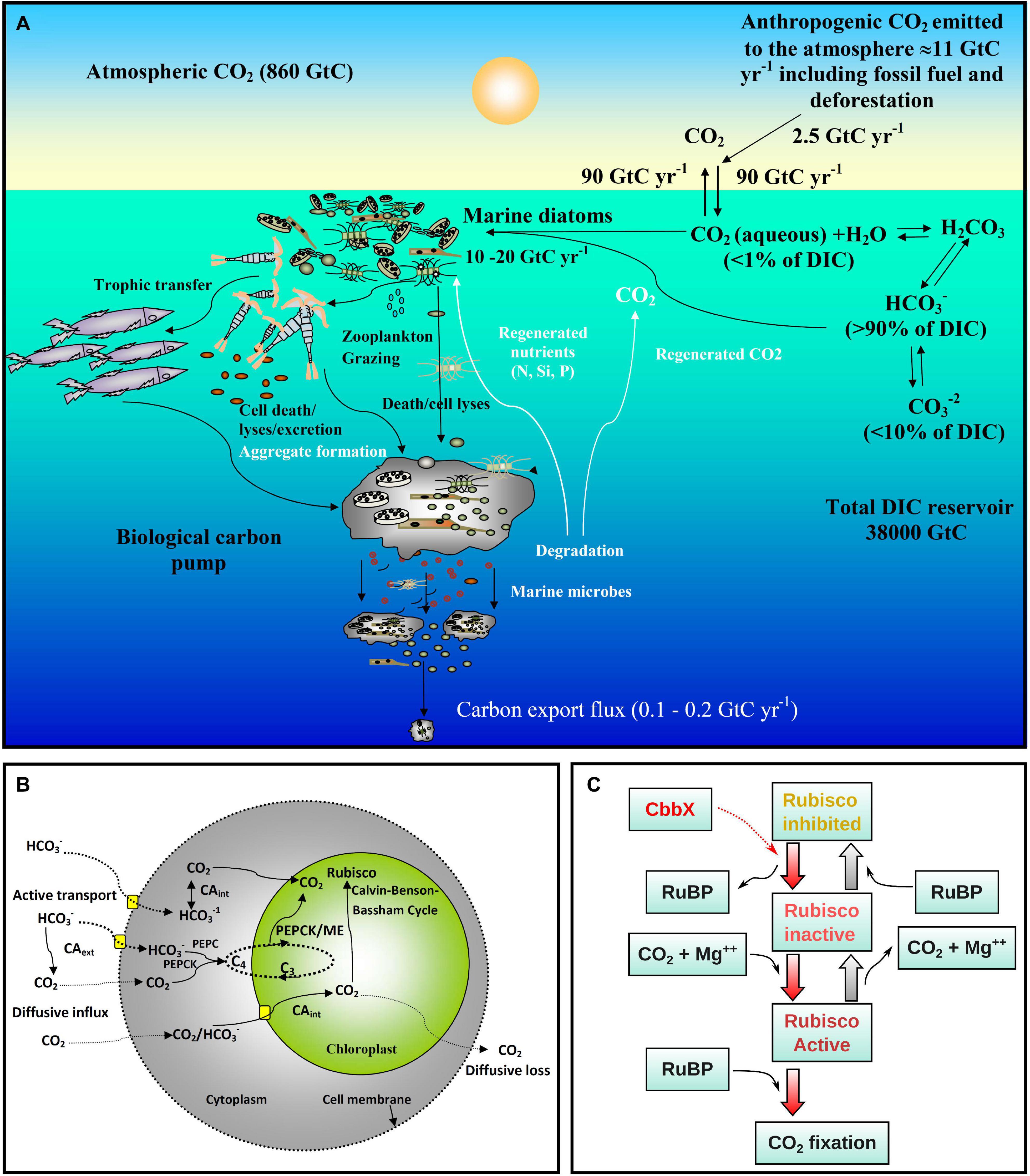



Frontiers Carbon Dioxide Concentration Mechanisms In Natural Populations Of Marine Diatoms Insights From Tara Oceans Plant Science




Latin Script Wikipedia




Dessous Sexy关键词链接



Relationships Between Carbon Fluxes And Environmental Factors In A Drip Irrigated Film Mulched Cotton Field In Arid Region



Auburn Edu



Arxiv Org



Actexmadriver Com




Dft U Calculations For Electronic Structural And Optical Properties Of Zno Wurtzite Structure A Review Sciencedirect
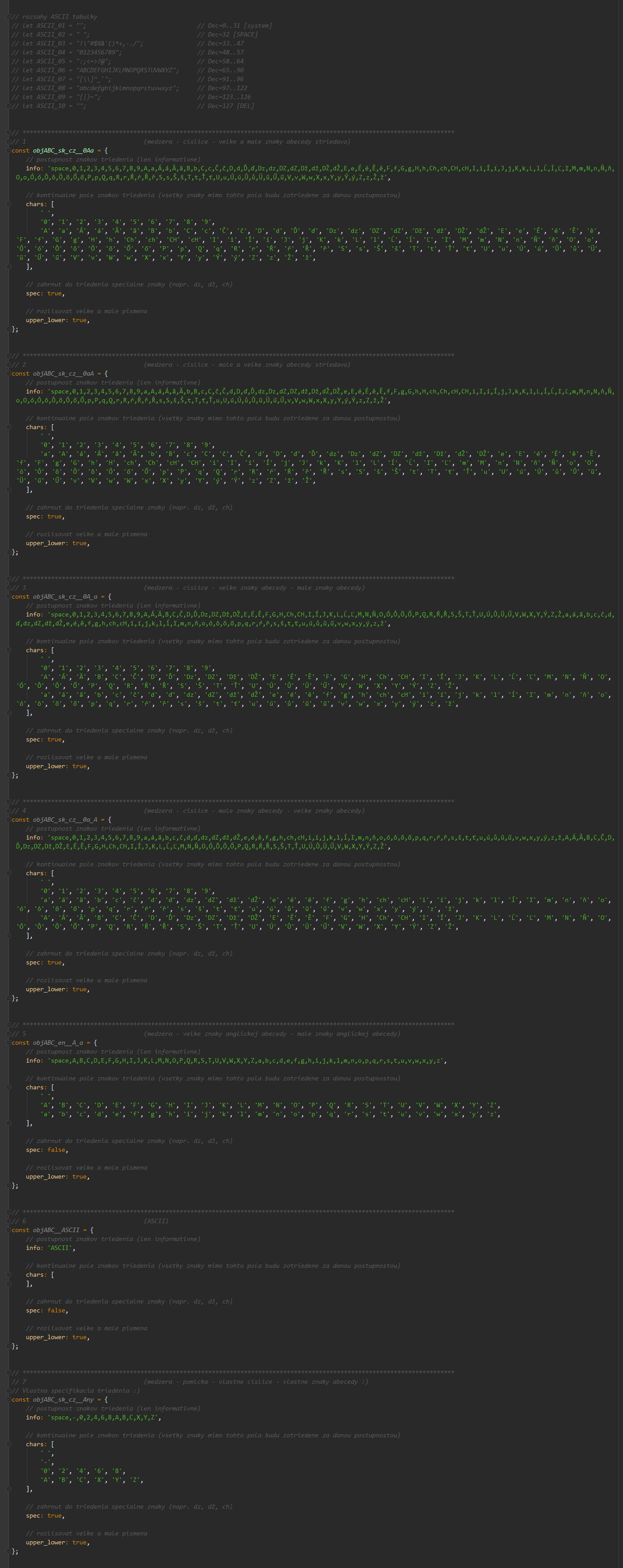



Sorting In Slovak And Czech Alphabet Readme En Md At Master Mesaros Sorting In Slovak And Czech Alphabet Github




What Does The Letter U Have To Do With W Dictionary Com




Transverse Sections Through 2 Dpf Zebrafish Larvae Stained With Ish Download Scientific Diagram




Applied Sciences Free Full Text A Chaotic System With Infinite Equilibria And Its S Box Constructing Application Html




The Polar Regions In A 2 C Warmer World




Warming And Elevated Ozone Induce Tradeoffs Between Fine Roots And Mycorrhizal Fungi And Stimulate Organic Carbon Decomposition




Basespintura Odt



Epa Gov




Solved In The First 2 Questions Use The Alphabet A B C C D Chegg Com




Spatial Variation In Biodiversity Loss Across China Under Multiple Environmental Stressors
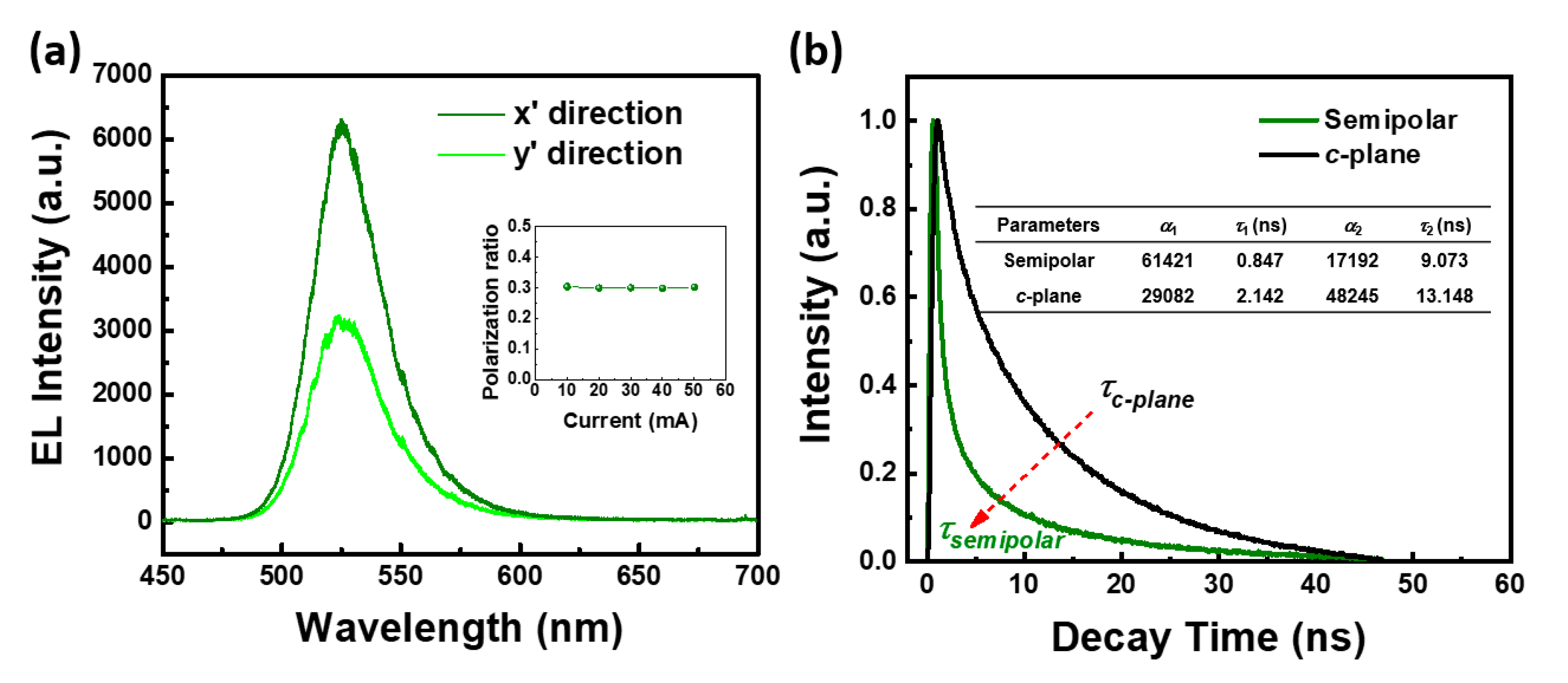



Applied Sciences Free Full Text Micro Led As A Promising Candidate For High Speed Visible Light Communication Html



Courts Wa Gov



C Span Org National Politics History Nonfiction Books



Courts Wa Gov




This Sculpture Holds A Decades Old C I A Mystery And Now Another Clue The New York Times



Karger Com



Alchemy Symbols




Eve At The District The Holidays Are Almost Here And We Can T Wait To Open Our Gifts Luckily This Picture Will Give Us All A Preview Of What We Can Expect
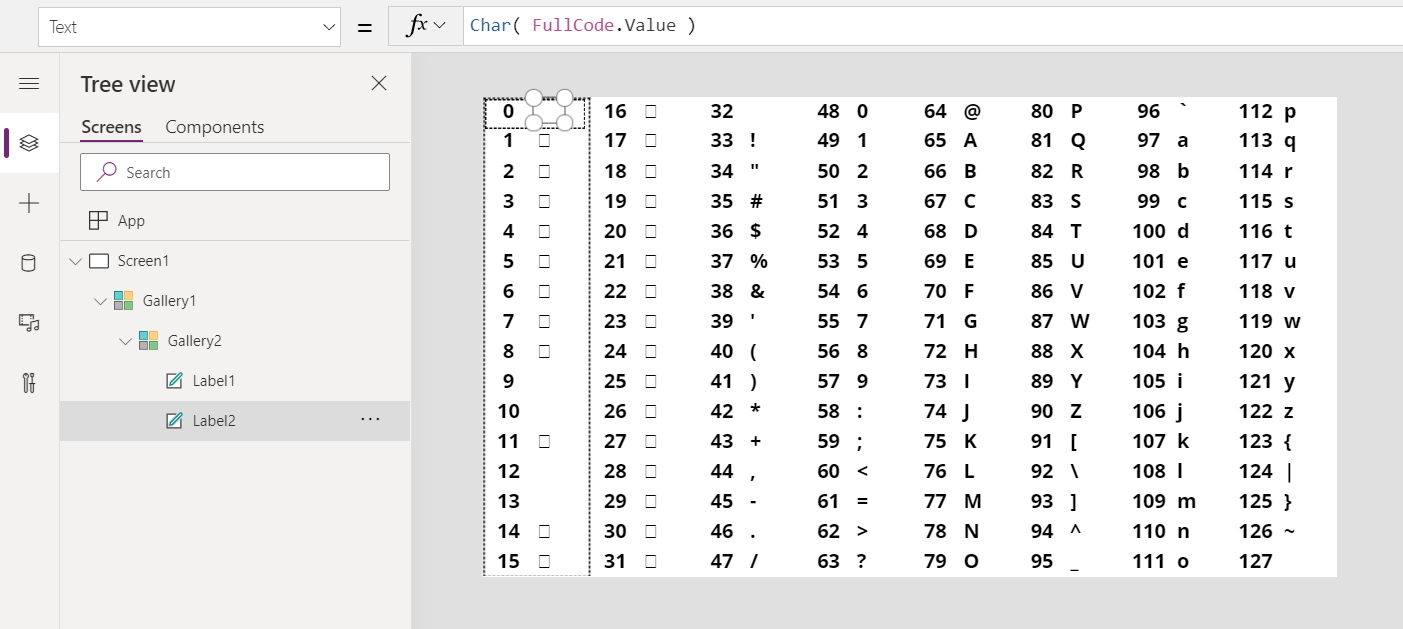



Char Function In Power Apps Power Apps Microsoft Docs
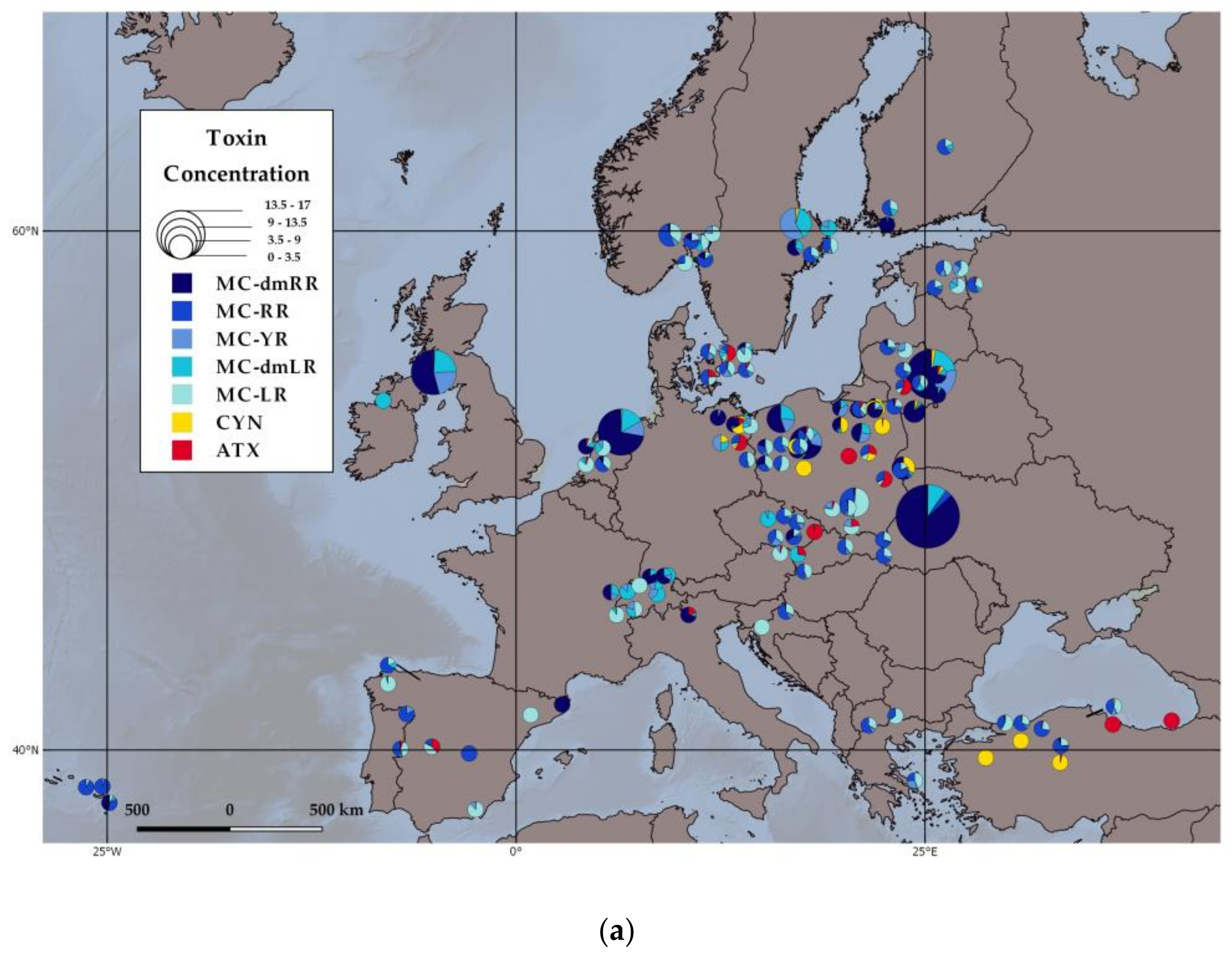



Toxins Free Full Text Temperature Effects Explain Continental Scale Distribution Of Cyanobacterial Toxins Html




Gsg 9 High Resolution Stock Photography And Images Alamy



Courts Wa Gov




Transmitter Code 1st Part Download Scientific Diagram



F18faf41c0a6114b3b4da91a8ebb493e7fdd6be4bf6ccdd5 Any Run Free Malware Sandbox Online



Navarra Es




How To Speak Chinese Maayot Bite Size Daily Chinese Stories




Iau Volume 8 Issue S290 Cover And Back Matter Proceedings Of The International Astronomical Union Cambridge Core



Ualberta Ca



Osti Gov



Aip Scitation Org




Pinyin Wikipedia



Arxiv Org



Degruyter Com



Stanford Edu




7 Chapter Nine Ideas Learn French Teaching French French Language Lessons



Courts Wa Gov




Ligature Writing Wikipedia
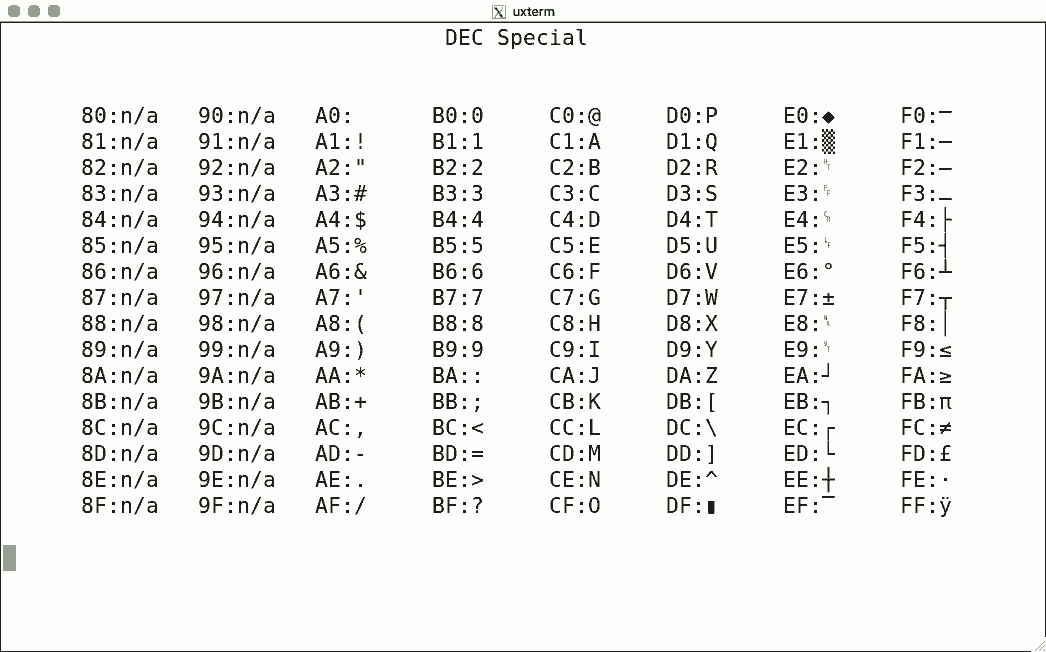



Luit Locale And Iso 22 Support For Unicode Terminals
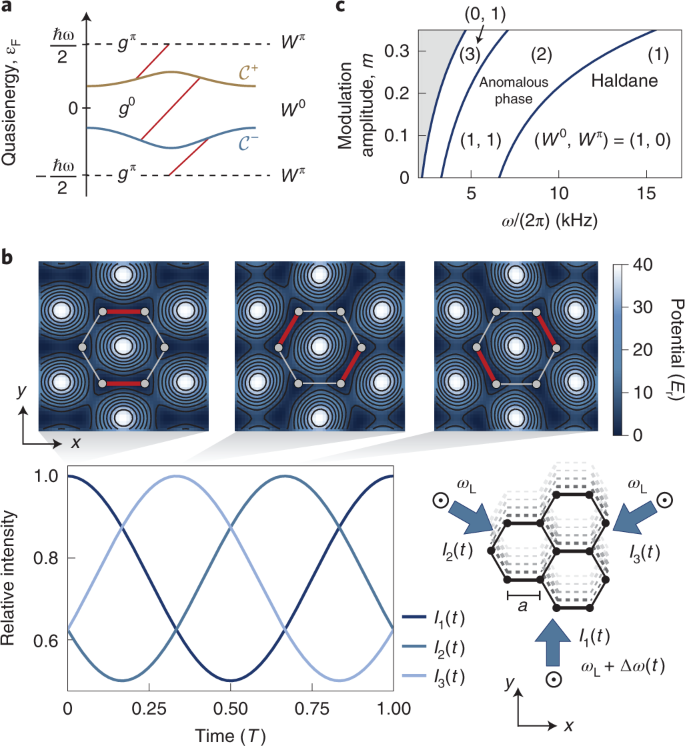



Realization Of An Anomalous Floquet Topological System With Ultracold Atoms Nature Physics



Math Iupui Edu



Shakopee K12 Mn Us



Cityofalliance Com



Armenian Alphabet Wikipedia
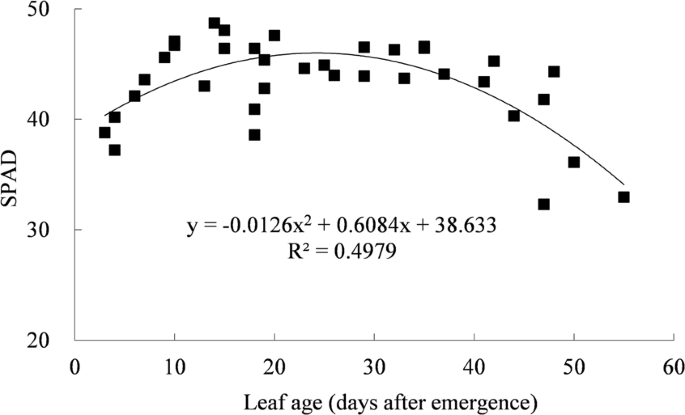



A General Non Rectangular Hyperbola Equation For Photosynthetic Light Response Curve Of Rice At Various Leaf Ages Scientific Reports
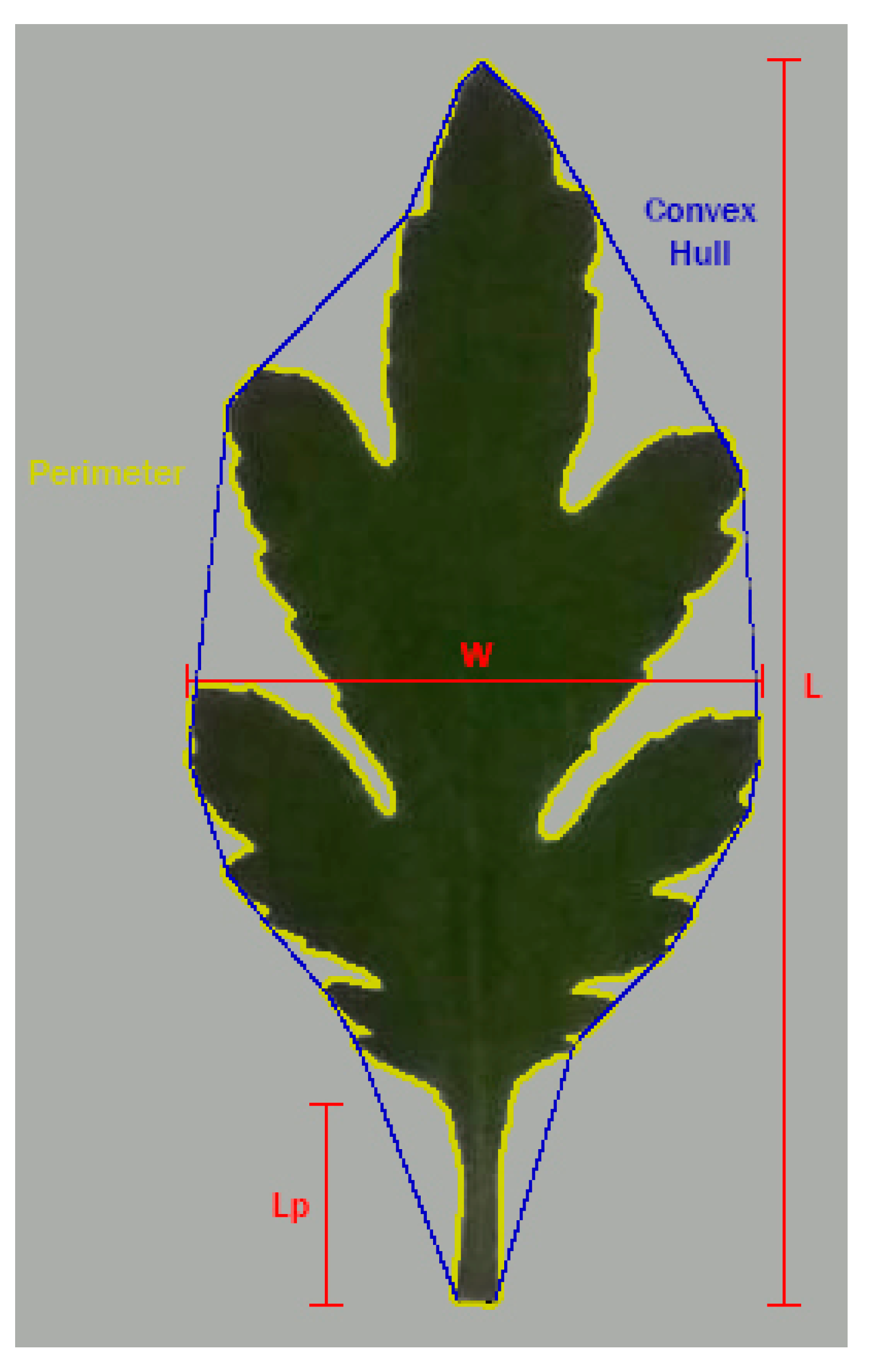



Agronomy Free Full Text Allometric Individual Leaf Area Estimation In Chrysanthemum Html



Degruyter Com
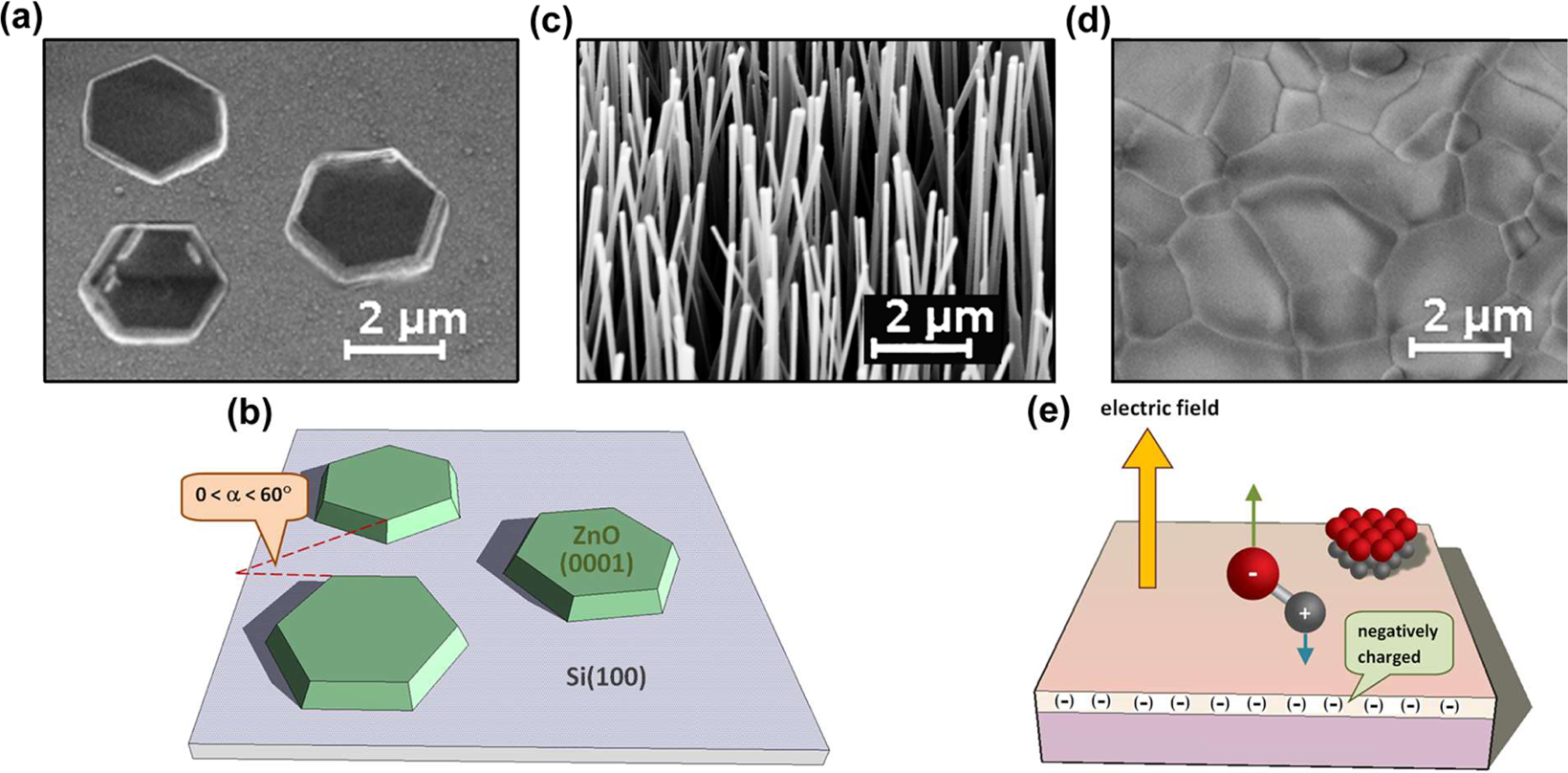



Why Do Nanowires Grow With Their C Axis Vertically Aligned In The Absence Of Epitaxy Scientific Reports
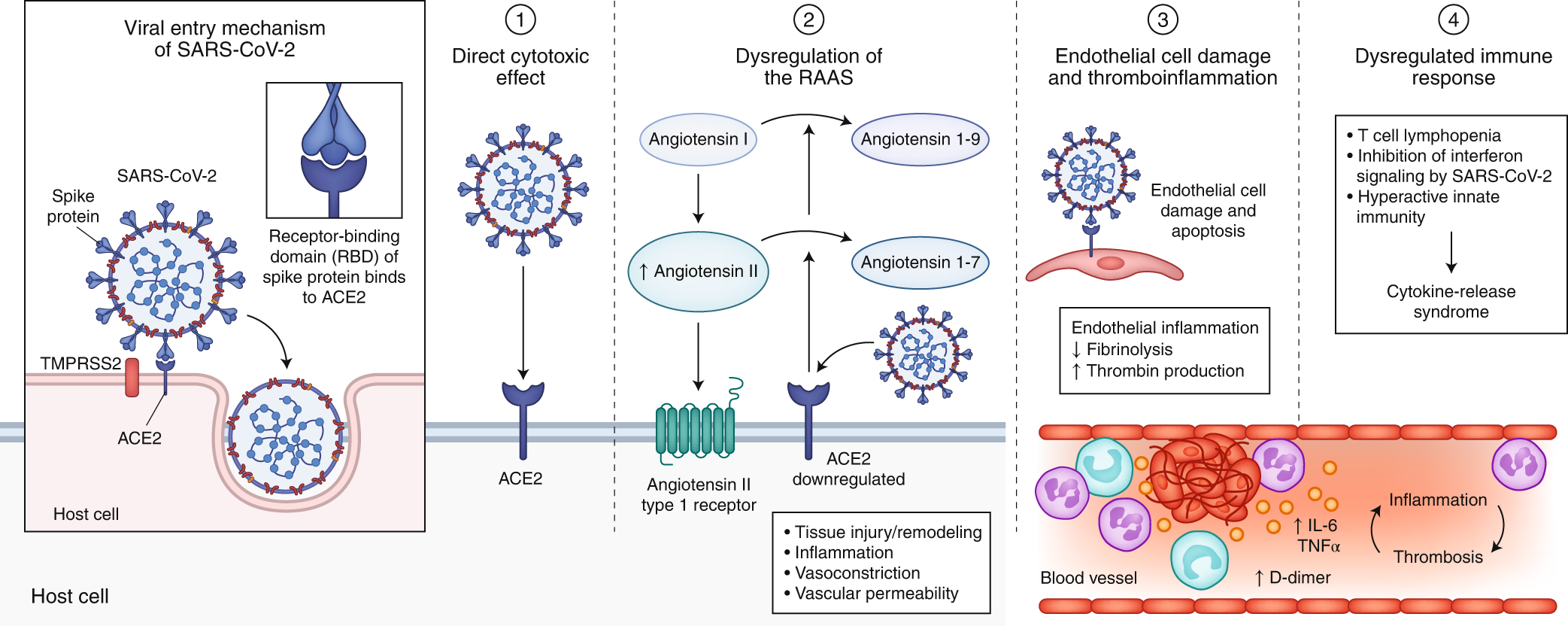



Extrapulmonary Manifestations Of Covid 19 Nature Medicine



Scriptsource Entry Phonetic Symbol Guide




Two Dimensional Mxenes From Morphological To Optical Electric And Magnetic Properties And Applications Sciencedirect
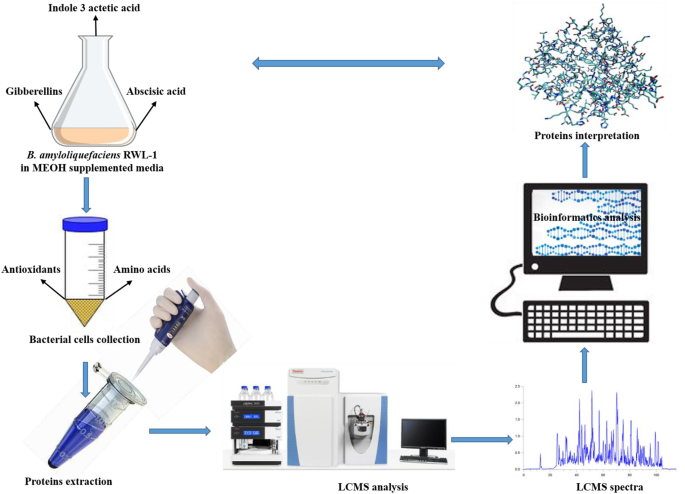



Metabolic And Proteomic Alteration In Phytohormone Producing Endophytic Bacillus Amyloliquefaciens Rwl 1 During Methanol Utilization Springerlink




List Of Unicode Characters Wikipedia




Ape Regina Branding On Behance



Ieeexplore Ieee Org




U Wikipedia




Rxtrrmntlt7yom



Courts Wa Gov



Scmapdb Sven Co Op Map Database




Ktowbekfc6v Fm
コメント
コメントを投稿